归并排序

归并排序（英语：Merge sort，或mergesort），是创建在归并操作上的一种有效的排序算法，效率为 O(nlog n) （大O符号）。1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。

归并操作（merge），也叫归并算法，指的是将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。该算法是一个稳定的排序算法。

基本思想:将待排序的元素分成大小大致相同的两个子集合,分别对两个子集合进行排序,最终将排好序的子集合合并成所要求的排好序的集合。

---

演示

一个归并排序的例子：对一个随机点的链表进行排序

归并排序算法示意图

---

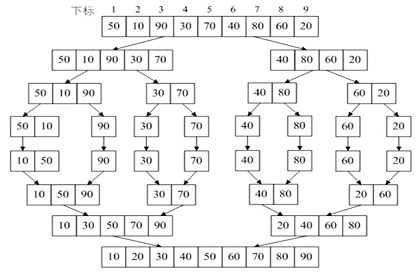
迭代法

1.申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
2.设定两个指针，最初位置分别为两个已经排序序列的起始位置
3.比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
4.重复步骤3直到某一指针到达序列尾
5.将另一序列剩下的所有元素直接复制到合并序列尾

递归法

1.原理如下（假设序列共有 n 个元素）：
2.将序列每相邻两个数字进行归并操作，形成 ceil(n/2)个序列，排序后每个序列包含n/2个元素
3.若此时序列数不是1个则将上述序列再次归并，形成 ceil(n/4)个序列，每个序列包含n/4个元素
4.重复步骤2，直到所有元素排序完毕，即序列数为1

---

Code

#include<iostream> 
using namespace std;
int a[20] = {0};
int n,length;

void merge(int a[],int left,int middle,int right,int temp[]){
	int i = left, j = middle + 1;
	int endOne = middle, endTow = right;
	int index = 0;
	while(i <= endOne && j <= endTow){
		if(a[i] <= a[j]){
			temp[index++] = a[i++];
		}else{
			temp[index++] = a[j++];
		}
	}
	
	while(i <= endOne){
		temp[index++] = a[i++];
	}
	
	while(j <= endTow){
		temp[index++] = a[j++];
	}
	
	for(int i = 0; i < index;i++){
		a[left+i] = temp[i];
	}
}

void sort(int a[],int left,int right,int temp[]){
	if(left < right){
		int middle = (left + right) / 2;
		sort(a,left,middle,temp);
		sort(a,middle + 1,right,temp);
		merge(a,left,middle,right,temp);
	}
}

int main(){
	cin >> n;//待排序元素个数
	int temp[n];
	for(int i = 0; i < n; i++){
		cin >> a[i];
	}	

	sort(a,0,n-1,temp);	
	for(int i = 0; i < n; i++){
		cout << a[i] << " ";
	}
	return 0;
}

---

参考

归并排序
白话经典算法系列之五 归并排序的实现（讲的真好）
【排序算法】归并排序(C++实现)