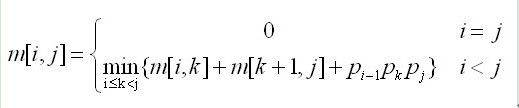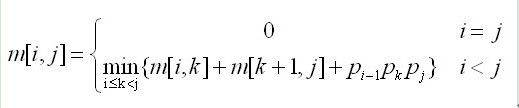矩阵连乘

题目

给定n个矩阵｛A1,A2,…,An｝，其中Ai与Ai+1是可乘的，i=1,2 ,…,n-1。如何确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少

---

动态方程

---

讲解

---

Code

#include<iostream>
#include <stdlib.h>
#define inf  99999999
#define X(x) x,x,x,x,x,x,x
using namespace std;

void matrixChain(int p[],int n,int m[][7],int s[][7]){
	for(int i = 1; i <= n;i++){
		m[i][i] = 0;
	}
	
	for(int r = 2; r <= n; r++){				//r为连乘矩阵的个数 
		for(int i = 1; i <= n - r + 1; i++){ 	//i表示连乘矩阵中的第一个
			int j = i + r - 1;   				//j表示连乘矩阵中的最后一个
			for(int k = i; k < j; k++){
				int temp = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
				if(temp < m[i][j]) {
					m[i][j] = temp;
					s[i][j] = k; 
				} 
			}
		}
	}
} 

void traceBack(int i, int j,int s[][7]){
	if(i==j)return;
	traceBack(i,s[i][j],s); 
	traceBack(s[i][j] + 1,j,s);
	cout<<"Multiply A "<<i<<","<<s[i][j];
	cout<<" and A "<<(s[i][j] + 1)<<","<<j<<endl;
}

void traceBackMore(int i, int j,int s[][7]){
	if(i==j){
		cout<<"A"<<i;
	}else{
		cout<<"(";
	traceBackMore(i,s[i][j],s); 
	traceBackMore(s[i][j] + 1,j,s);
		cout<<")";
	}
}

int main(){
	int p[] = {30,35,15,5,10,20,25}; // 7个P值,6个矩阵 ,n为6 
	int n = 6;
	int m[7][7] = {X(X(inf))};
	int s[7][7];

	matrixChain(p,n,m,s); 
	cout<<endl;
	traceBack(1,n,s);
	cout<<endl;
	traceBackMore(1,n,s);
	return 0;
}

---

参考

矩阵连乘 动态规划
矩阵连乘 动态规划 详解