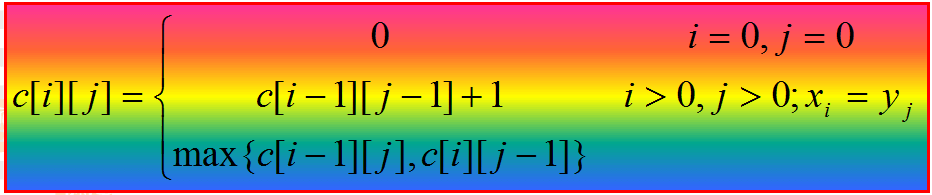最长公共子序列(LCS)

Preface

这学期算法课的某次计蒜客留的作业,有一题便是求最长公共子序列。
不得不吐槽的是,放题目的人居然取的题名是 最长共公子串。

子序列和子串的区别是子串是连续的,而子序列的元素可以是间隔开的。无论子串还是子序列各个元素中的相对次序还是和原符号串一样的。

LCS的定义:一个数列 S，如果分别是两个或多个已知数列的子序列，且是所有符合此条件序列中最长的，则 S称为已知序列的最长公共子序列。

---

简单起见,本文讨论的是两个序列的最长公共子序列。也是一个dp水题,根据最优子结构性质有以下的递归关系

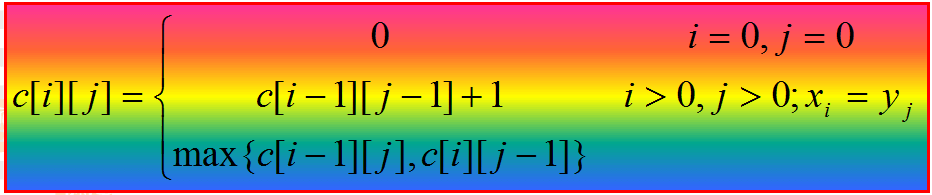
上图最后一行是max{c[i-1][j],c[i][j-1]} i,j>0;xi != yi;

设有两个序列X = {X1,X2,X3….,Xm} , Y ={Y1,Y2,Y3….,Ym};c[i][j]记录Xi和Yi的最长公共子序列长度,s[i][j]记录c[i][j]的值是由哪一个子问题的解得到的( 比如把c[i-1][j-1]] + 1记作1,c[i-1][j]]记作2,c[i][j-1]]记作3 )。

---

Code

#include<iostream> 
#define MAX 2017
using namespace std;

int c[MAX][MAX],s[MAX][MAX];

int maxLength(string a,string b,int aLength,int bLength){
	int i,j;
	for(i = 1;i <= aLength; i++){c[i][0]=0;}
	for(i = 1;i <= bLength; i++){c[0][i]=0;}
	for(i = 1; i <= aLength; i++){
		for(j =1; j <= bLength;j++){
		//这里要-1是因为,字符串的第一个字符是存储在0下标对应的位置的 
			if(a[i-1] == b[j - 1]){  
				c[i][j] = c[i-1][j-1] + 1;
				s[i][j] = 1;
			}else if(c[i-1][j] >= c[i][j-1]){
				c[i][j] = c[i-1][j];
				s[i][j] = 2;
			}else{
				c[i][j] = c[i][j-1];
				s[i][j] = 3;
			}
		}
	}
	return c[aLength][bLength];
}

void LCS(int i,int j,string a){
	if(i == 0 || j == 0)return;
	if(s[i][j] == 1){
		LCS(i-1,j-1,a);
		cout<<a[i - 1];
	}else if(s[i][j] == 2){
		LCS(i-1,j,a);
	}else{
		LCS(i,j-1,a);
	}
}

int main(){
	string a,b;
	cin >> a >>b;
	int aLength = a.length(),bLength = b.length();
	cout<<maxLength(a,b,aLength,bLength)<<endl;
	LCS(aLength,bLength,a);
	return 0;
}