最大子段和

问题介绍

最大子段和问题又叫最大子数列问题。该问题的目标是在数列的一维方向找到一个连续的子数列，使该子数列的和最大。例如，对一个数列−2, 1, −3, 4, −1, 2, 1, −5, 4，其连续子数列中和最大的是4, −1, 2, 1,其和为6。

该问题最初由布朗大学的Ulf Grenander教授于1977年提出，当初他为了展示数字图像中一个简单的最大似然估计模型。不久之后卡内基梅隆大学的Jay Kadane提出了该问题的线性算法。

---

Kadane算法

Kadane算法扫描一次整个数列的所有数值，在每一个扫描点计算以该点数值为结束点的子数列的最大和（ 正数和 ）。该子数列由两部分组成：以前一个位置为结束点的最大子数列、该位置的数值。因为该算法用到了“最佳子结构”（以每个位置为终点的最大子数列都是基于其前一位置的最大子数列计算得出）， 该算法可看成动态规划的一个例子。

---

将长度为n的目标序列存储在一个数组中,设为a。设数组b为如下

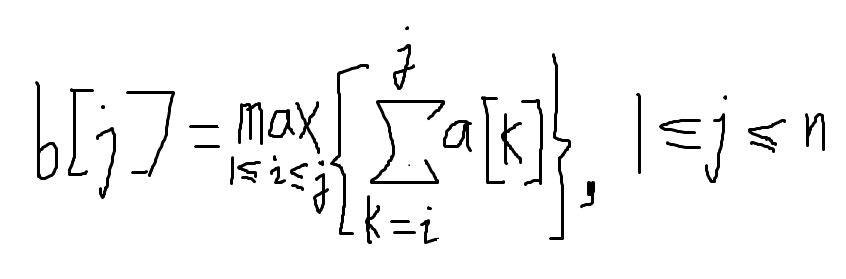
由b[j]的定义易知,当b[j-1] > 0时 b[j] = b[j-1] + a[j],否则b[j] = a[j]。由此可得计算b[j]的动态规划递归方程

b[j] = max{b[j - 1] + a[j],a[j]}, 1 <= j <= n

---

Code

#include<iostream>
#define MAX 1000 
using namespace std;
void sum(int a[],int n){
	int result = 0,b = 0;
	int begin = 0,end = 0;//记录最大子段的起始，终止下标 
	for(int i = 0; i < n;i++){
		if(b > 0){
			b += a[i];
		}else{
			b = a[i];
			begin = i;
		}
		if(b > result){
			result = b;	
			end = i;
		}
	}
	
	//输出数组最大字段 
	 for(int i = begin; i <= end; i++){
	 	cout<<a[i]<<" ";
	 }
	cout<<endl;
	cout<<result<<endl;
}

int main(){
	int a[MAX],n;
	cin >> n;//数组元素个数 
	for(int i = 0; i<n; i++){
		cin >> a[i];
	}
	sum(a,n);
	return 0;
}

---

参考

最大子数列问题