活动安排问题

问题描述

这里我就用截的PPT里的图片简单描述

---

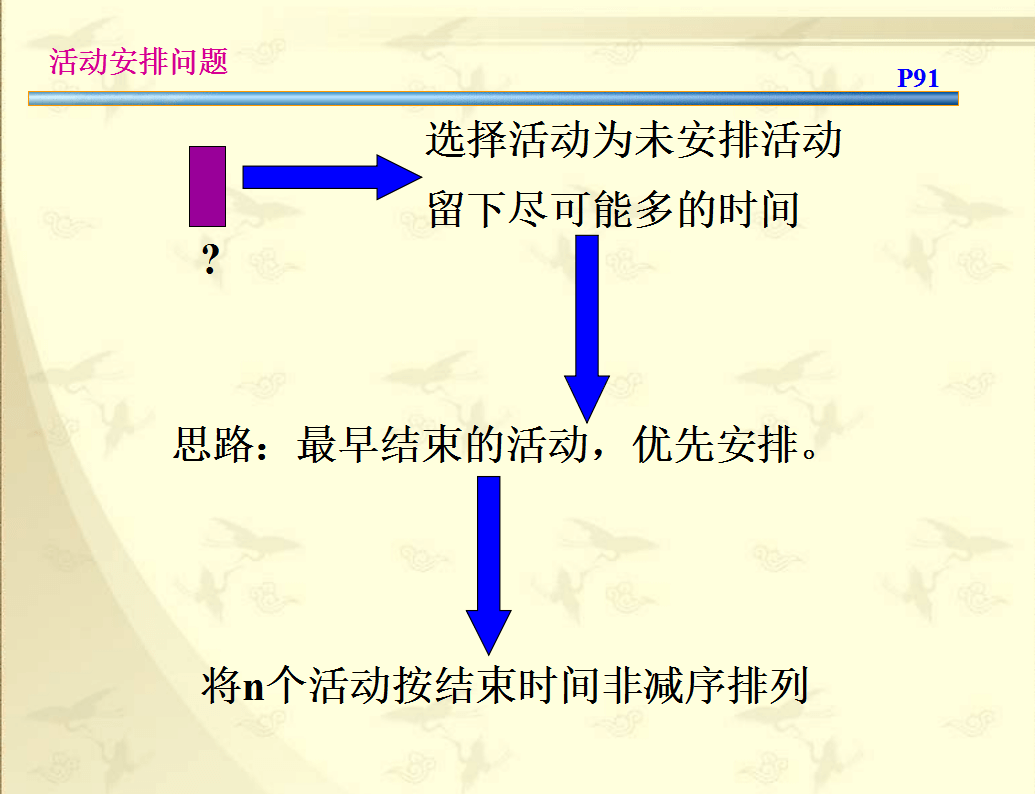
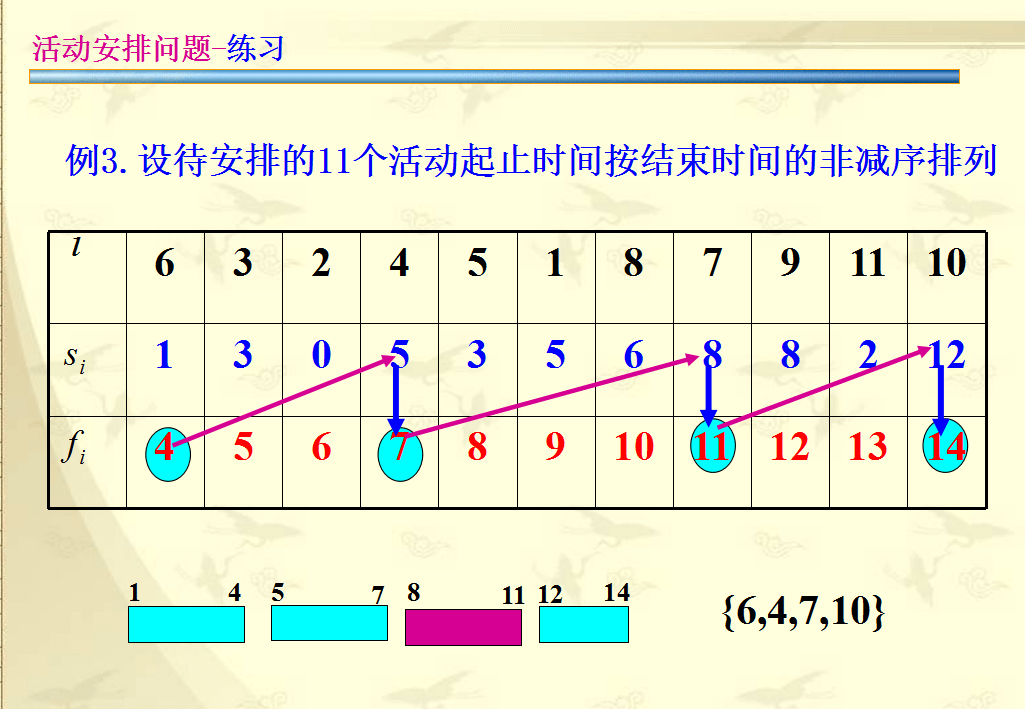
题解

上面的图片已经讲述得很清楚了,这里做些总结和补充。 这里的贪心策略是越早结束的活动越先安排,这样才能尽可能多的安排更多的活动,即上面图片中所谓的最大的相容活动子集合。

要先对输入数据排序。 在下面的参考代码中,我使用的结构体来存储输入数据。 排序是按照如下规则进行排序的:结束时间越小(早),越靠前。倘若结束时间相同,则开始时间越大(晚),越靠前。因为这样可以节约出更多的时间。

main函数中的j是记录最近一次被选中的活动。当前活动的开始时间大于等于j活动的结束,即可以被选中。

---

#include<iostream>
#include<algorithm>
using namespace std;

struct node{
	int start;
	int end;
	bool a;//记录活动是否被选中 
}activity[2017];

bool cmp(node x,node y){
	if(x.end < y.end)return true;
	//x.start > y.start是因为结束时间一样,x.start越大,可以节约出更多的时间 
	if(x.end == y.end && x.start > y.start)return true;
	return false;
} 

int main(){
	int n;
	cin >> n;
	for(int i = 0; i < n; i++){
		cin>>activity[i].start>>activity[i].end;
	} 
	sort(activity,activity+n,cmp);
	activity[0].a = true;//选中第一个活动 
	int count = 1; //可以选择的活动数量 
	int j = 0;//记录最近一次选中的活动 
	for(int i = 1; i < n; i++){
		if(activity[i].start >= activity[j].end){
			activity[i].a = true;
			j = i;
			count++;
		}else{
			activity[i].a = false;
		}
	} 
	
	cout<<"最大活动数量"<<count<<endl;
	for(int i = 0; i < n; i++){
		if(activity[i].a == true){
			cout<<activity[i].start<<"  "<<activity[i].end<<endl;
		}
	}
}